Les notions de base

Une enquête statistique porte sur un ensemble de personnes ou d’objets : population (constituée d’individus).

Lorsque la population est impossible à étudier dans son ensemble, on étudie un échantillon.

L’enquête vise à mettre en évidence une certaine particularité de cette population : cette particularité est appelée caractère ou variable.

Si le caractère est mesurable, il est dit quantitatif (on peut lui associer un nombre : taille, année de naissance, âge) sinon il est qualitatif (couleur des yeux, région d’habitation..).

Un caractère peut être discret ou continu :

• Discret = Il peut prendre des valeurs « isolées » (nombre d’enfants)
• Continu = Il peut prendre toutes les valeurs d’un intervalle de nombres réels (somme d’argent)

Les résultats sont mis en forme dans des tableaux et/ou des graphiques.

La moyenne

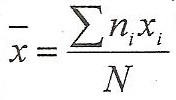
La médiane

Me est la valeur d’un caractère quantitatif qui partage l’effectif total de la population en deux groupes égaux (= effectifs égaux ou de fréquences égales à 50%).

L’écart type

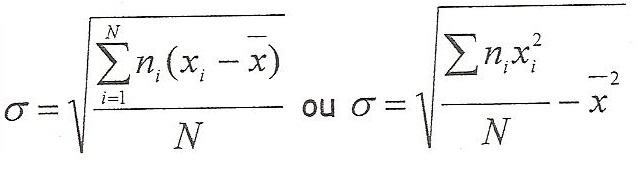
La fréquence

fi = ni/N

Centre de classe

[a ; b[ -> xi = (a+b)/2

Amplitude de classe

[a ; b[ -> b-a

Quartile

Notés Q1, Q2 et Q3 sont les trois valeurs de la variable qui partagent la listes des valeurs ordonnées en quatre groupes de même effectif. Rq : Q2 = Me

Interquartile

C’est la différence entre les quartiles Q3 et Q1 noté : I = Q3-Q1

[Q1 ;Q3] contient la moitié des valeurs observées.

[Q1 ;Me] et [Me ;Q3] contient le quart des valeurs observées.

Représentation graphique

Effectifs cumulés croissants -> On prend les bornes de droites de classes.

Effectifs cumulés décroissants ->On prend les bornes de gauche des classes.

Diagramme en bâton -> Chaque donnée est représentée par un bâton de hauteur correspondant à l’effectif ou la fréquence.

Ajustement affine

Méthode de Mayer : La droite passe par G1 et G2, les deux points moyens des deux nuages partiels d’importance équivalente. La droite (G1G2) est appelée droite de Mayer, elle passe par G.

Méthode des moindres carrés : C’est déterminer quelle droite est suceptible de remplacer « au mieux » le nuage de points. C’est la droite d’ajustement de y par rapport à x ; on la note : Dy/x

Cette droite passe par le point G(moy x ; moy y) et a pour équation :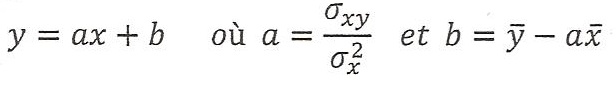

Variables aléatoires discrètes

Loi Binomiale

Loi Normale

Loi Normale centrée réduite

Passage d’une loi normale à la loi centrée réduite

Approximation d’une loi binomiale par une loi normale

Pour n suffisamment grand, une variable aléatoire X qui suit la loi B(n ;p) suit approximativement la loi normale N(np ; √npq).

=> Il faut (si l’énoncé le demande) appliquer une correction de continuité, qui consiste à remplacer chaque valeur xi prise par X par l’intervalle :

[xi – 0,5 ; xi + 0,5]

Opérations sur les variables aléatoires indépendantes

Somme de deux va

Somme de deux va indépendantes suivants des lois normales

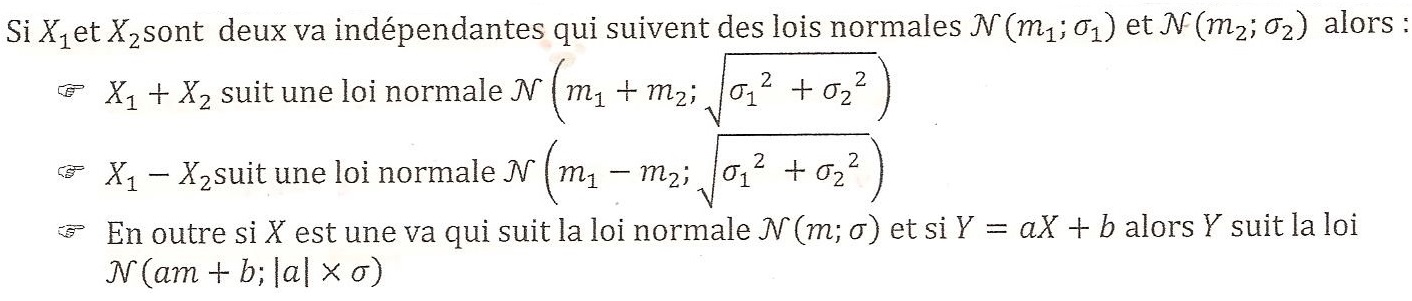
-> Voir aussi les suites

---