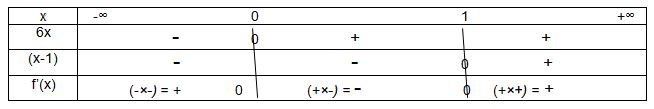Pour étudier le sens de variations d’une fonction, il faut étudier le signe de sa dérivée.

Limite d’une fonction

• La limite d’une fonction polynôme en +∞ (respectivement en -∞) est égal à la limite en +∞ (respectivement en -∞) du terme de plus haut degré.
• La limite d’une fonction rationnelle en +∞ (respectivement en -∞) est égal à la limite en +∞ (respectivement en -∞) du quotient (fraction) des termes de plus haut degré du numérateur et du dénominateur.

Asymptotes

• Si lim f(x) = +/- ∞ pour x = a => asymptote verticale d’équation x = a
• Si lim f(x) = b pour x = +/- ∞ => asymptote horizontale d’équation y = b
• Si lim [f(x) – (ax + b)] = 0  pour  x -> +/- ∞ => asymptote oblique d’équation y = ax + b

Variation d’une fonction

Soit une fonction définie sur un intervalle I, et admettant sur cet intervalle une dérivée f’.

• Si pour tout x de I, on a : f’(x) ≥ 0 alors f est croissante sur I.
• Si pour tout x de I, on a : f’(x) ≤ 0 alors f est décroissante sur I.

=> On en déduit donc les tableaux de variations à partir de l’étude de signe de la dérivée.

Résoudre une équation du second degré

Y = ax² + bx + c

Calcul du discriminant: ∆= b²-4ac

1^er cas : ∆ < 0 : Le polynôme n’a pas de racine.

2^ème cas : ∆ > 0 : Le polynôme a 2 racines :

• x1 = (-b -√∆) / 2a
• x2 = (-b +√∆) / 2a

> Dans ce cas le polynôme peut se factoriser : ax² + bx + c => a(x-x1)(x-x²)

3^ème cas : ∆ = 0 : Le polynôme a une racine double : α = -b / 2a

> Dans ce cas le polynôme peut se factoriser : ax² + bx + c => a(x-α)²

=> Dans tous les cas le polynôme est toujours du signe de a sauf à l’intérieur des racines :

Variation d’une fonction                                               

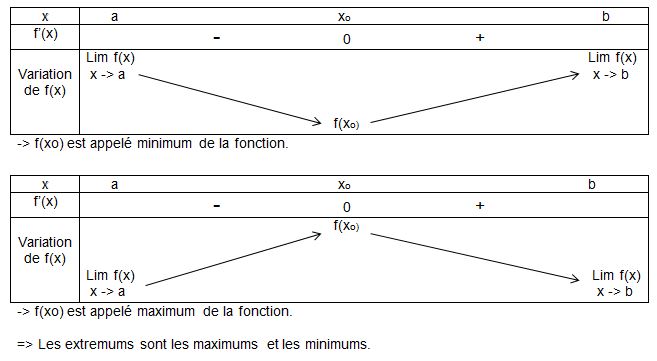
Pour le tableau de variation il faut indiquer toutes les valeurs pour lesquelles la fonction f(x) = 0 pour cela voir calcul discriminant.-> f(xo) est appelé minimum de la fonction.-> f(xo) est appelé maximum de la fonction. => Les extremums sont les maximums et les minimums.

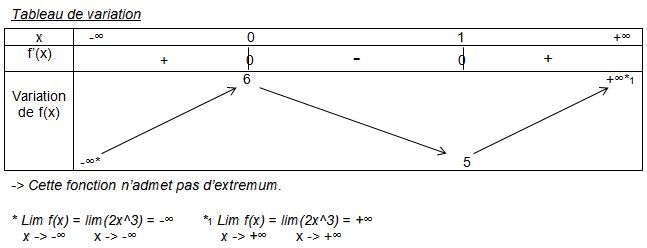
Pour le tableau de variation il faut indiquer toutes les valeurs pour lesquelles la fonction f(x) = 0 pour cela il faut factoriser l’équation dérivée si c’est une fonction simple ou alors faire le calcul discriminant pour un polynôme du second degré.

Exemple

Dresser le tableau de variations de la fonction f(x) = 2x^3 – 3x^2 + 6

-> On dérive f(x) : f’(x) = 3 × 2x^(3-1) – 2 × 3x^(2-1) = 6^2 – 6^x

Il faut factoriser pour avoir la dérivée sous forme de multiplication : f’(x) = 6x(x-1)

-> Pour vérifier si la factorisation est bonne il faut développer la factorisation pour vérifier si on retombe sur l’équation de base de la dérivée : 6x × x + 6x × (-1) = 6x^2 – 6^x

Tableau de signe

Il faut indiquer toutes les valeurs pour lesquelles la fonction f(x) = 0

C’est une fonction simple donc résolution d’équation simple des facteurs : 6x = 0 <-> x=0 / x-1 = 0 <-> x = 1

=> Si c’était un polynome de seconde degré « y = ax² + bx + c » alors calcul du discriminant (au dessus)

---